KONDO Ryoichi近藤 諒一

原子力発電は、私たちの生活に必要な電力の供給のみならず、データセンターや半導体工場など、安定供給が求められる産業分野にも適しています。こうした背景から国内でも原子力発電への関心が高まっており、政府が2025年に策定した第7次エネルギー基本計画ではカーボンニュートラルを達成しつつ、増加する電力需要に対応するため、原子力発電を持続的に活用する方針が示されています。

原子力を用いて安全に発電するためにはその挙動を正確に予測することが欠かせません。原子炉では中性子と原子核の反応によって熱が生まれます。さらに冷却材となる水の流れや燃料の温度変化など、複数の物理現象が同時に起こります。原子炉の挙動を数値シミュレーションで正確に再現するには、それぞれの物理現象を詳細かつ正確に計算する必要があります。しかしながら、これを実現するためには膨大な計算量が必要であり、限られた計算資源で効率的に計算することが求められます。

そこで私は、原子炉内で重要な役割を果たす中性子輸送の挙動を効率的に計算するための研究をしています。精度の高い計算手法としてモンテカルロ法が知られていますが、統計的な手法であるため得られる解には統計誤差が付随し、これを小さくするためには計算負荷が大きくなることが課題となっています。一方で、近年の研究では、固有直交分解という手法を用いて分布の特徴を抽出することにより、原子炉内の複雑な中性子の分布を少ない情報量で表現できることがわかってきました。そこで私は、固有直交分解をモンテカルロ法に組み合わせることにより高精度な計算を効率的に行うことを試みました。燃料棒が並ぶ燃料集合体１体のみの比較的小さい体系で得られる中性子の分布から特徴となる情報を抽出し（図1）、抽出した情報を用いて複数の燃料集合体の分布を再現できることがわかりました（図2）。また、従来手法と比べて統計誤差の小さい解を得ることに成功し、計算量削減の可能性を示す重要な知見となりました。

今後は、提案手法による中性子輸送計算を熱流動計算と組み合わせた連成計算への応用を目指しています。一連の研究によって中性子輸送計算の精度向上に取り組み、原子力発電のさらなる安全性向上に貢献したいと考えています。

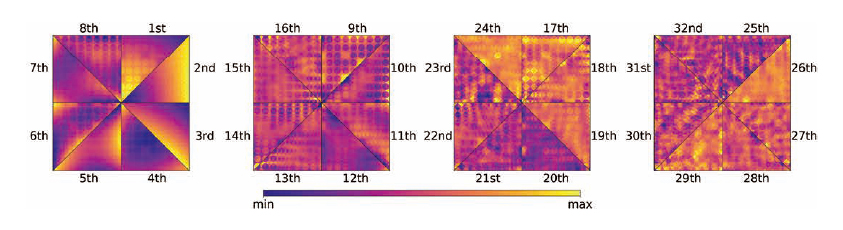
図1 複数条件の単一集合体計算の中性子束分布を特異値分解して得られた基底ベクトル

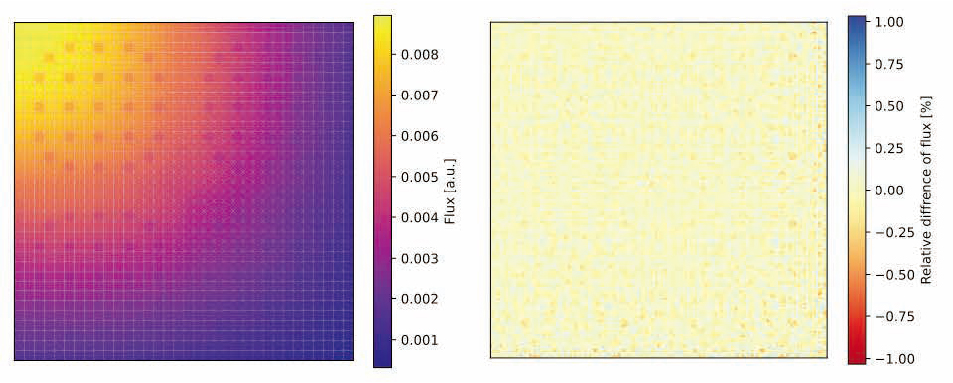
図2 基底ベクトルで再構成された複数集合体の中性子束分布（左）と参照解との差異（右）