Satake Yuki佐竹 祐樹

工学・情報学など多くの応用分野において、様々な数理上の問題や方程式を数値的に解くことが求められます。特に近年、科学技術の発展と共に、より大規模な計算が必要となってきています。したがって、そういった問題や方程式を解くために、計算機上でいかに効率的に計算するかというのが重要な課題の一つとなります。私は、特に行列方程式と呼ばれる問題を研究対象として、効率的数値解法の構築に向けた研究を行っています。具体的には、対象とする行列方程式を「数値計算をする上で扱いやすい等価な方程式に変換」するための理論の構築を行っています。理論を構築することができれば、元の行列方程式の解を、等価な方程式の求解のみによって得ることが可能になります。これにより、行列方程式に対する効率的な解法につながる可能性があります。

たとえば、振動解析などに現れる★-congruence Sylvester方程式と呼ばれる行列方程式があります。この行列方程式は、未知行列とその転置もしくは共役転置が同時に含まれており、これが計算上の難しさの要因の一つとなっていました。私たちの研究では、この行列方程式を、未知行列の転置も共役転置も含まない行列方程式に変換することを考えました。通常、この行列方程式に正則行列を乗じるなどの変換を行っても未知行列の転置や共役転置を消すことはできません。そこで、★-congruence Sylvester方程式がベクトル化と線形化によって連立1次方程式の形に書き換えられることを利用して、この連立1次方程式の行列構造に着目した線形作用素の構築を行いました。この線形作用素によって変換された連立1次方程式を再び行列化させることで、未知行列の転置も共役転置も含まない行列方程式（一般化Sylvester方程式）に変換できることを示しました（図1）。この変換によって、解法の計算量を削減できることも分かっています。

現在は、一般化Sylvester方程式に対する反復法のための前処理の開発に取り組んでいます。私たちは、一般化Sylvester方程式のベクトル化によって得られる連立１次方程式のテンソル構造に着目し、この構造を保存させるような前処理の構築を行っています。これにより、対象とする一般化Sylvester方程式を収束性の良い別の行列方程式に変換することが可能となり、反復法の高速化が期待できます。実際に本研究で構築した前処理を一般化Sylvester方程式に対する反復法に適用することで、いくつかの数値例に対して収束の改善が確認できました（図2）。今後は、前処理に現れる計算の効率化や、大規模並列計算環境のためのアルゴリズム開発など、本手法の実用化に向けた研究を行っていく予定です。

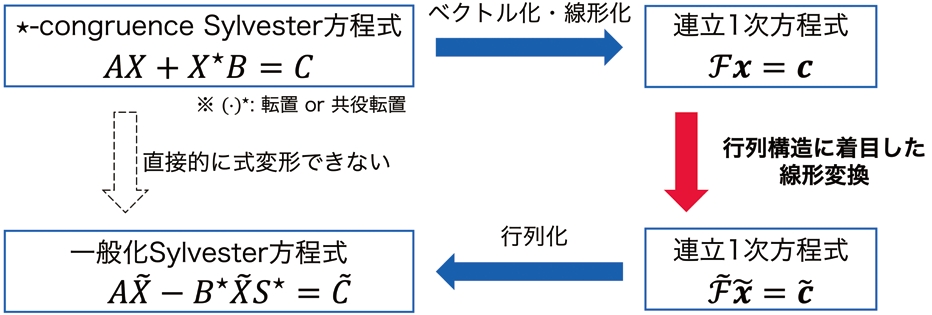
図1　★-congruence Sylvester方程式から一般化Sylvester方程式への変形の概要

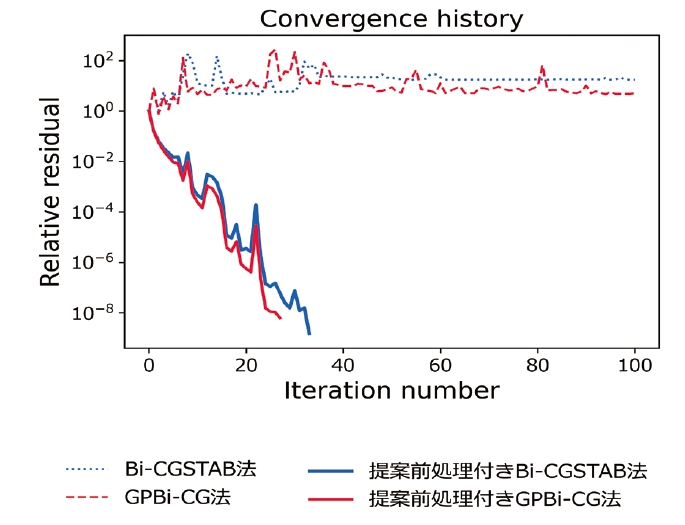
図2　前処理なし反復法と提案前処理付き反復法の収束履歴の比較